Bicubic Bézier Patches and Surfaces Tutorial

In the following tutorial you will learn how to manage and generate bicubic Bezier surfaces and how to concatenate multiple patches using the vl::BezierPatch and vl::BezierSurface classes.

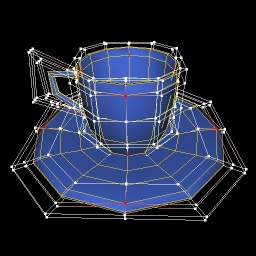
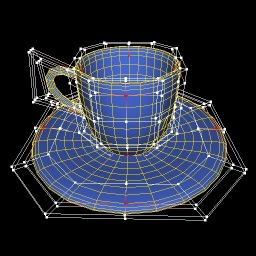
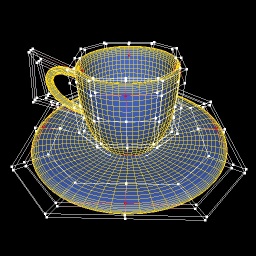
Newell's tea cup rendered using 26 4x4 Bézier patches with increasing tessellation level from left to right. The dots and the white lines represent the control points of the patches, the red dots represent the corner control points that are guaranteed to touch the Bézier surface.

From Wikipedia [http://en.wikipedia.org/wiki/Bézier_surface]:

"Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modelling. As with the Bézier curve, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive, and for many applications, mathematically convenient."

"Bézier surfaces were first described in 1972 by the French engineer Pierre Bézier who used them to design automobile bodies. Bézier surfaces can be of any degree, but bicubic Bézier surfaces generally provide enough degrees of freedom for most applications."

As you will se the actual code dealing with the Bezier patches is less than ten lines of code! The majority of the code is dedicated to generate the patch data, to setup the effects, to manage the user input and so on.

[From App_BezierSurfaces.cpp]

class App_BezierSurfaces: public BaseDemo
{
public:
  App_BezierSurfaces(): mDetail(10) {}

  virtual String appletInfo()
  {
    return BaseDemo::appletInfo() + 
    "- Up/Down Arrow = increase/decrease the Bezier surface tessellation detail.\n" +
    "- Space         = toggle control points visibility.\n" +
    "\n";
  }

  void initEvent()
  {
    vl::Log::notify(appletInfo());

    /* 2 pass shader: 1 = solid, 2 = wireframe */

    ref<Effect> fx = new Effect;

    fx->shader()->enable(EN_LIGHTING);
    fx->shader()->gocLightModel()->setTwoSide(true);
    fx->shader()->enable(EN_DEPTH_TEST);
    fx->shader()->gocLight(0)->setLinearAttenuation(0.025f);
    fx->shader()->gocMaterial()->setDiffuse(royalblue);

#if defined(VL_OPENGL)
    fx->lod(0)->push_back( new Shader);
    fx->shader(0,1)->enable(EN_DEPTH_TEST);
    fx->shader(0,1)->gocPolygonOffset()->set(-1.0f, -1.0f);
    fx->shader(0,1)->enable(EN_POLYGON_OFFSET_LINE);
    fx->shader(0,1)->gocPolygonMode()->set(PM_LINE, PM_LINE);
    fx->shader(0,1)->gocDepthMask()->set(false);
    fx->shader(0,1)->gocColor()->setValue(gold);
#endif

    /* Generate random Bézier patches

    - The simplest bicubic Bézier patch requires 4x4 = 16 control points: A, B, C, D, E, F, G, H, I, L, M, N, O, P, Q, R
    - The Bézier surface is guaranteed to touch only the 4 corner control points A, D, O and R.

    A---B---C---D
    |   |   |   |
    E---F---G---H
    |   |   |   |
    I---L---M---N
    |   |   |   |
    O---P---Q---R

    - You can concatenate two bicubic Bézier patches to form a larger suface by sharing their control points like this:

       patch 1     patch 2
    A---+---+---B---+---+---G
    |   |   |   |   |   |   |
    +---+---+---C---+---+---+
    |   |   |   |   |   |   |
    +---+---+---D---+---+---+
    |   |   |   |   |   |   |
    F---+---+---E---+---+---H

    - In this case the two patches share the control points B, C, D and E.
    - As we can see the total control points needed are 28 = (2 (patches along x) * 3 + 1) * (1 (patches along y) * 3 + 1)
    - Also in this case the Bézier surface is guaranteed to touch only the 6 corner control points A, B, E, F, G and H.

    If we wanted to concatenate 3x2=6 Bézier patches in a single BezierPatch we would do the following:
    int x = 3;
    int y = 2;
    ref<BezierPatch> patch = new BezierPatch( x*3+1, y*3+1 ); // using the formula above
    for(int y=0;y<patch->y();++y)
      for(int x=0;x<patch->x();++x)
        patch->at(x,y) = ... fill x/y control point ...

    */

    /* Add Bézier patches to our Bézier surface */

    // Load newell teaset
    std::string teapot_txt = String::loadText("models/newell_teaset/teapot").toStdString();
    std::stringstream sstr(teapot_txt);
    int patchnum = 0;
    sstr >> patchnum;
    std::vector<int> patch_idx;
    for(int i=0; i<patchnum; ++i)
    {
      for(int j=0; j<16; j++)
      {
        int p = 0;
        sstr >> p;
        patch_idx.push_back(p);
      }
    }
    int vertnum;
    sstr >> vertnum;
    std::vector<vec3> verts;
    verts.resize(vertnum);
    for(int i=0; i<vertnum; ++i)
    {
      float x, y, z;
      sstr >> x >> y >> z;
      verts[i] = vec3(x, z, -y);
    }

    // Instance our Bézier surface
    mBezier = new BezierSurface;

    // Add loaded patches
    for(int i=0; i<patchnum; ++i)
    {
      ref<BezierPatch> patch = new BezierPatch(4,4);
      for(int j=0; j<16; ++j)
      {
        int idx = patch_idx[j+16*i]-1;
        patch->points()[j] = verts[ idx ];
      }
      mBezier->patches().push_back(patch.get());
    }

    // Define the subdivision detail
    mBezier->setDetail(mDetail);
    
    // Generate the actual geometry using the current patches and detail
    mBezier->updateBezierSurface(false);
    
    // Compute the normals as we have lighting activated
    mBezier->computeNormals();
    
    // Add the Bézier surface to our scene
    sceneManager()->tree()->addActor(mBezier.get(), fx.get(), NULL);

#if defined(VL_OPENGL)
    // Show the control points
    showPatchControlPoints(mBezier.get());
#endif

    // position the camera to nicely see the teapot in the scene
    trackball()->adjustView( sceneManager(), vec3(0,0,1)/*direction*/, vec3(0,1,0)/*up*/, 1.0f/*bias*/ );
  }

  /* 
    up/down arrow = increase/decrease the Bézier surface tessellation detail
    space         = toggle control points visibility
  */
  void keyPressEvent(unsigned short ch, EKey key)
  {
    BaseDemo::keyPressEvent(ch,key);
    if (key == Key_Up)
    {
      ++mDetail;
      mDetail = clamp(mDetail, 2, 64);
      mBezier->setDetail(mDetail);
      mBezier->updateBezierSurface(false);
      mBezier->computeNormals();
      mBezier->setBufferObjectDirty(true);
    }
    else
    if (key == Key_Down)
    {
      --mDetail;
      mDetail = clamp(mDetail, 2, 64);
      mBezier->setDetail(mDetail);
      mBezier->updateBezierSurface(false);
      mBezier->computeNormals();
      mBezier->setBufferObjectDirty(true);
    }
    else
    if(key == Key_Space)
    {
      if (sceneManager()->tree()->actors()->find(mCtrlPoints_Actor.get()) == -1)
        sceneManager()->tree()->actors()->push_back(mCtrlPoints_Actor.get());
      else
        sceneManager()->tree()->actors()->erase(mCtrlPoints_Actor.get());
    }
  }

  /* Generates the geometry to render the control points */
  void showPatchControlPoints(BezierSurface* bezier)
  {
    ref<Effect> fx = new Effect;
    fx->shader()->enable(EN_DEPTH_TEST);
    fx->shader()->gocPolygonMode()->set(PM_LINE, PM_LINE);
    fx->shader()->gocLineWidth()->set(1.0f);
    fx->shader()->gocPointSize()->set(5.0f);

    ref<Geometry> geom = new Geometry;

    int istart = 0;
    std::vector<fvec3> verts;
    std::vector<fvec4> colos;
    for(unsigned ipatch=0; ipatch<bezier->patches().size(); ++ipatch)
    {
      const BezierPatch* p = bezier->patches()[ipatch].get();
      for(int ix=0; ix<p->x()-3; ix+=3)
      for(int iy=0; iy<p->y()-3; iy+=3, istart+=16)
      {
        verts.push_back((fvec3)p->at(ix+0,iy+0)); colos.push_back(red);
        verts.push_back((fvec3)p->at(ix+0,iy+1)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+0,iy+2)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+0,iy+3)); colos.push_back(red);

        verts.push_back((fvec3)p->at(ix+1,iy+0)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+1,iy+1)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+1,iy+2)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+1,iy+3)); colos.push_back(white);

        verts.push_back((fvec3)p->at(ix+2,iy+0)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+2,iy+1)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+2,iy+2)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+2,iy+3)); colos.push_back(white);

        verts.push_back((fvec3)p->at(ix+3,iy+0)); colos.push_back(red);
        verts.push_back((fvec3)p->at(ix+3,iy+1)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+3,iy+2)); colos.push_back(white);
        verts.push_back((fvec3)p->at(ix+3,iy+3)); colos.push_back(red);

        ref<DrawArrays> da = new DrawArrays(PT_POINTS, istart,16);
        ref<DrawElementsUInt> de = new DrawElementsUInt(PT_QUADS);
        de->indexBuffer()->resize(4*9);
        unsigned int quads[] = { 0,1,5,4, 4,5,9,8, 8,9,13,12, 1,2,6,5, 5,6,10,9, 9,10,14,13, 2,3,7,6, 6,7,11,10, 10,11,15,14 };
        for(int q=0; q<4*9; ++q)
          quads[q] += istart;
        memcpy(de->indexBuffer()->ptr(), quads, sizeof(quads));
        geom->drawCalls()->push_back(de.get());
        geom->drawCalls()->push_back(da.get());
      }
    }

    ref<ArrayFloat3> vert_array = new ArrayFloat3;
    geom->setVertexArray(vert_array.get());
    vert_array->initFrom(verts);

    ref<ArrayFloat4> cols_array = new ArrayFloat4;
    geom->setColorArray(cols_array.get());
    cols_array->initFrom(colos);

    geom->makeGLESFriendly();

    mCtrlPoints_Actor = sceneManager()->tree()->addActor(geom.get(), fx.get(), NULL);
  }

protected:
  ref<BezierSurface> mBezier;
  ref<Actor> mCtrlPoints_Actor;
  int mDetail;
};

// Have fun!